←Piecewise expressionsConstruct operands→

2.8.3 Generators

A generator is an expression that summarizes a larger expression through parameterization. Myron provides two kinds of generators: for collections and for series.

Generators can be expanded symbolically using Distribute or evaluated using Evaluate . When distributed, an expanded value can be produced if the domains are manifest. When evaluated, an expanded value can be produced if the templates and domains can be bound.

The descriptions provided here address the syntax of generators. For more information on collections, see §6.2. For more information on how to work with generators, see §6.3.

2.8.3.1 Series Generators

Syntactically, series generators use a form similar to definite integration: an introductory symbol followed by a three-element list of expressions, a concluding ⅆ and an index variable. The first two expressions provide lower and upper bounds for the generator. The third expression provides an element template for terms in the series. The introductory symbols are ∑ for summation and ∏ for product. Figure 2.42 displays the standard form of series-generator syntax along with some variations.


(a) Series
(b) Bounds
Figure 2.42 Series generators and bounds
Generator Input Alternate Display
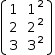
Summation ∑0,n,i^2 ⅆi ∑i=0,n,i^2 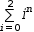∑0, 2, i^nⅆi
Product ∏2,n+1,i^2 ⅆi ∏i=2,n+1,i^2 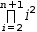∏2, n+1, i^2ⅆi
Figure 2.43 Generator examples

The examples in the Alternate column of Figure 2.43 more closely resemble mathematical notation. When the alternate syntax is used, the trailing ⅆ and variable are no longer needed (and are not allowed). While this is closer to the usual mathematical notation for generators, a generator of this form must be parenthesized if it participates in a larger expression. In contrast, parenthesization is not required for the standard form of generator because it is delimited naturally by ⅆ.

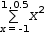
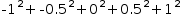
A second syntactic variation provides control over the increment value. When a value other than the default increment of 1 is needed, another expression can be inserted just before the template expression. For example, the input ∑-1,1,.5,x^2$dx displays as ∑-1, 1, 0.5, x^2ⅆx. After Distribute , the generator produces -1^2+-0.5^2+0^2+0.5^2+1^2.

2.8.3.2 Generalized Series Generators

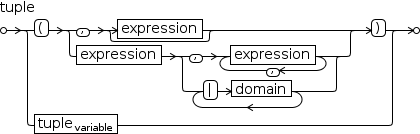
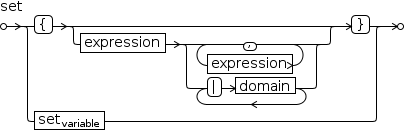
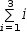
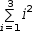
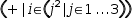
Syntactically, a generalized series generator looks like a tuple generator with a binary operator in place of the template. The summation ∑1, 3, iⅆi could be replaced by the generalized series (+|i∈1, 3). However, the summation ∑1, 3, i^2ⅆi requires a composition of generators (+|i∈(j^2|j∈1, 3)).

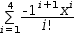
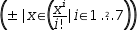
When used with the ± operator, a generalized series generates an alternating series. For example, the first few terms of the Taylor series for sin x are given by the summation series generator ∑1, 4, -1^(i+1)⋅x^i÷i !ⅆi. Using the generalized series generator, an equivalent expression is entered as (±|x∈(x^i÷i!|i∈1,7,2)) and displayed as (±|x∈(x^i÷i !|i∈1, 7, 2)). The series expansion can be seen by applying Distribute to produce x^1÷1 !-x^3÷3 !+x^5÷5 !-x^7÷7 !.

2.8.3.3 Collection Values and Generators

Tuple, set and matrix values use comma-separated lists of expressions to denote elements of collections. However, when there is a relationship between elements, the list can be condensed using a generator. These generators use a syntax taken from linear-algebra and set-theory notation. Like series generators, collection generators require a template expression to specify the form of individual elements. This is followed by one or more generator domain expressions, which can be another collection generator, a collection value, a domain literal or a predicate. All of this is enclosed in delimiters that give the type of the generated collection.


(a) Tuple value and generator
(b) Domains
(c) Interval domains
Figure 2.44 Tuple value, generator and domains

Tuples. Figure 2.44 gives the syntax of both tuple values and tuple generators. The paths that traverse commas denote tuple values: collections with explicit elements. Note from the diagram that a tuple value always contains at least one comma. This distinguishes it from a simple parenthesized expression. There is even a path containing a comma and no expressions, to denote an empty tuple.

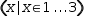
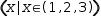
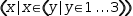
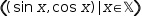
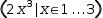
The path in Figure 2.44 (a) that traverses at least one domain denotes a tuple generator. To illustrate, a simple tuple generator is entered as (x|x∈1,3) and displayed as (x|x∈1, 3). This generator uses an interval as the domain. The domain could instead be a collection value, as in (x|x∈(1, 2, 3)), another generator, as in (x|x∈(y|y∈1, 3)), or an axis domain, as in ((, sin x, cos x)|x∈𝕏). The template could be a real expression, as in (2⋅x^3|x∈1, 3), or a collection expression, as in ((x, x^2)|x∈1, 3).

Syntactic FormDisplay Form
R1(x|x∈1,3)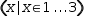(x|x∈1, 3)
R2(x|x∈(1,4)co)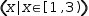(x|x∈(1, 3)co)
R3(x|x∈1,3,.5)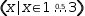(x|x∈1, 3, 0.5)
R4(x|x∈3,1,-1)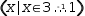(x|x∈3, 1, -1)
P1(x|1≤x≤3)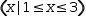(x|1≤x≤3)
P2(x|(1≤x)∧(x<4))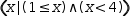(x|(1≤x)∧(x&lt;4))
C1(x|x∈(1,2,3))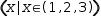(x|x∈(1, 2, 3))
C2(x|x∈cʈ)(x|x∈cʈ)
A1(x^2|x∈𝕏)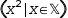(x^2|x∈𝕏)
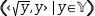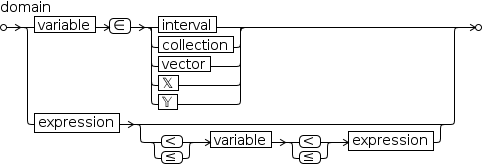
A2((√y,y)ʋ|y∈𝕐)((√y, y)ʋ|y∈𝕐)
Figure 2.45 Interval, predicate, collection and axis domains

Figure 2.45 contains examples showing the use of different domain expressions in a tuple generator. Most of the examples generate the same tuple. Example R2 makes use of interval notation. R3 uses a non-integer step value and R4 uses a negative step value. The predicate examples P1 and P2 infer a control variable from the predicate expression. The first of these has a more efficient implementation than the second and may be preferred for that reason. Example C1 creates a tuple of scalars from the elements of another tuple, but the source could be any collection. In example C2, the source is another tuple; in this example the generator is not manifest and therefore cannot be distributed, but with a definition of 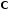cʈ elsewhere in the workspace, the generator can be evaluated. Examples A1 and A2 show tuples with axis domains. The domain variables 𝕏 and 𝕐 are only available for binding in the plotter and as a result the generator cannot be distributed in the workspace.

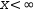
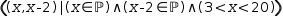
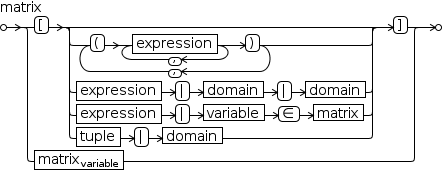
Predicates used in tuple generators can be almost any expression that contains one variable and evaluates to a Boolean result. The implementation tests a range of values bounded by constants inferred from the predicate. However, there are some limits to the use of predicates. A generator with a predicate like x&lt;∞ is not iterable because it would generate an infinite tuple. In contrast, a generator like

((x, x-2)|(x∈ℙ)∧(x-2∈ℙ)∧(3&lt;x&lt;20)),

 


which generates tuples of adjacent small primes, is evaluable, albeit not efficiently because the test for primeness is not particularly efficient.

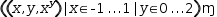
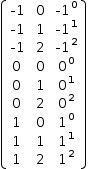
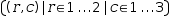
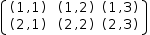
The syntax diagram in Figure 2.44 shows that a tuple generator can have more than one domain. The domains are composed by nesting trailing domains within leading domains. For example, ((x, y, x^y)|x∈-1, 1|y∈0, 2)ɱ contains a tuple generator with a cast to matrix. Simplification produces

[(, -1, 0, -1^0), (, -1, 1, -1^1), (, -1, 2, -1^2), (0, 0, 0^0), (0, 1, 0^1), (0, 2, 0^2), (1, 0, 1^0), (1, 1, 1^1), (1, 2, 1^2)].

 


Sets. The syntax for sets (Figure 2.46) uses braces instead of parentheses. Any of the tuple examples given above could be converted to set examples simply by changing the outer parenthesis to braces (except for the empty tuple value). Moreover, the type of the domain collection does not need to be the same as the type of the generator. A set can be changed into a tuple by using it as the collection domain in a tuple generator: (t|t∈sʂ).

Figure 2.46 Set value and generator

Matrices. Figure 2.47 shows three forms of matrix generator. The first form of matrix generator () uses two domain expressions that iterate over the rows and columns. [(r, c)|r∈1, 2|c∈1, 3] distributes to a matrix of tuples:

[((1, 1), (1, 2), (1, 3)), ((2, 1), (2, 2), (2, 3))].

 


Figure 2.47 Matrix value and generator

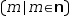
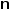
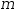
The second form of matrix generator uses just one domain expression which references another matrix. The simplest form of this, [m|m∈nɱ] uses the dimensions and elements of nɱ to reproduce the elements. The template m is bound to each element in turn. The generator can be used to modify the elements of a matrix by changing the expression in the template. For example, [(x, x^2)|x∈[(, 1), (, 2), (, 3)]] distributes to [(, (1, 1^2)), (, (2, 2^2)), (, (3, 3^2))].

The third form of matrix generator also uses just one domain expression (which cannot be a matrix domain) and a tuple in the template. The domain generates the rows and the template describes what should be in each row. For example, [(x, x^2)|x∈(1, 2, 3)] distributes to [(1, 1^2), (2, 2^2), (3, 3^2)].